-Prólogo

El cálculo integral tiene su origen en el estudio del área de figuras planas; las fórmulas para el cálculo de las áreas de triángulos y rectángulos eran ya conocidas en la Grecia clásica, así como la de los polígonos regulares previa descomposición en triángulos.

El problema se plantea a la hora de calcular áreas de figuras limitadas por líneas curvas. Euclides (300 a.C.) sigue los trabajos de Eudoxio (400-355 a.C.) para calcular el área del círculo por el método de exhaución, es decir, inscribiendo en él sucesivamente polígonos con más lados. La suma de estas áreas se aproximaba cada vez más al área del círculo, estando en el «límite» el valor exacto. Demostró además que, dados dos círculos de áreas A1 y A2 y  radios r1 y r2, se verificaba que  y que  , siendo k una constante que Arquímedes llamó 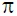 y cuyo valor dijo hallarse entre .  Arquímedes (287-212 a.C.) halló también el área encerrada por un arco de parábola y la cuerda correspondiente, cosa realmente difícil en aquel tiempo,  ya que no se disponía del álgebra formalizada ni de la geometría analítica. El método utilizado era el de agotamiento, esto es, se encaja el área entre dos polígonos, uno inscrito en la región y otro circunscrito a la región.
Desde los griegos hasta el siglo XVII poco se hizo con relación al cálculo de áreas y volúmenes de figuras limitadas por líneas o superficies cerradas.
Pascal, Fermat y Leibniz comienzan un estudio engarzado con el cálculo diferencial; así pues, aunque históricamente se estudian los primeros elementos del cálculo integral antes que el diferencial, en el siglo XVII se estudian y configuran a la par, relacionándose por medio de muchos e importantes resultados.

Por esto la mayoría de los autores empiezan exponiendo, en primer lugar, al menos, las primeras nociones de cálculo diferencial, antes de comenzar el estudio del cálculo integral.

Veamos cuál sería la metodología a emplear para el cálculo de áreas de superficies como las siguientes:

Podemos considerar el lado curvo como la gráfica de una función y = f(x).
Si llamamos A al área de la figura, se cumplirá que:

Pero esto no nos aporta en muchas ocasiones una idea suficientemente aproximada del valor de A. Supongamos que el intervalo [a, b] lo dividimos en tres partes:

Entonces, el valor del área que buscamos queda acotado entre dos cantidades:

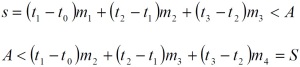
Si aumentamos el número de puntos en la división de [a, b], cada vez se irán acercando más los valores de s y S, de modo que nos darán una información más precisa sobre A.
Ésta sería la idea intuitiva, puesto que trabajaremos con funciones reales de variable real.